ステッピング・モータなどでモーションコントロールさせる際の加速・減速の手法として
台形駆動・三角駆動や曲線駆動があります。
1.台形駆動とは
モーションコントロールの位置決め制御を行うに於いて、A点からB点に位置決めをさせる場合。
A-B間の移動量Dの移動(位置決め動作)行う場合。
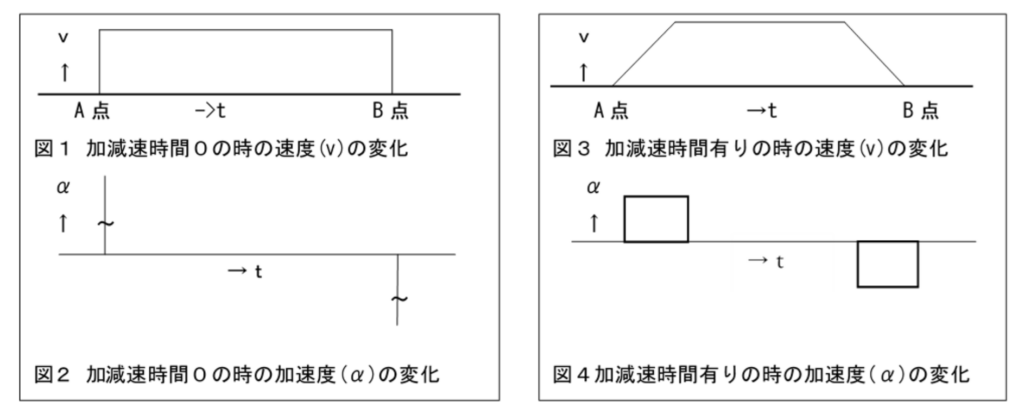
注1)時間:t(横軸) 速度:v(縦軸) 加速度:α(縦軸)
注2)加速度α=(v-v0)/t
1.スタート地点A点から移動量DのB点に移動(位置決め)を行うのに速度vを加速・減速時間0で動作を行った場合が
図1です。 注2)の式より加速度αは分母のtが限りなくゼロに近くなるので、計算結果は理論上では限りなく
∞(無限大)となりかなりの振動や衝撃となります。 また、ステッピング・モータであれば、速度が自起動周波数
※1以上で使用すると脱調状態※2となり正常な動きが出来なくなります。
2.その衝撃・振動を軽減させる方法は、図3の様に速度vに到達するのに任意の時間をかけて行う台形駆動による加減
手法があります。この手法を用いれば先ほどに比べ図4の様に加速度の最大値を抑えることができます。
加速―>等速―>減速この様子を図にすると図3の様な台形の形になるので台形駆動と呼ばれているようです。
またこの時正しく減速加速停止させるためには加速時に要した移動量を【d1】とすると【D-d1】の位置から減速を行い
ます、この減速開始点が早くても遅くてもいけません。このポイントの計算を適切に行う事が重要です。
2.三角駆動とは
同じくA点からB点に移動させる場合で移動距離が短く速度が最高速度に達しないと台形駆動にならず、図5に示す様な時は三角駆動となります。 その時の加速度は、図6の様に+αからーα(加速から一転して減速)に変化し、より一層の振動や衝撃の要因となり時には脱調状態となり正常な動作が出来なくなる事も有ります。
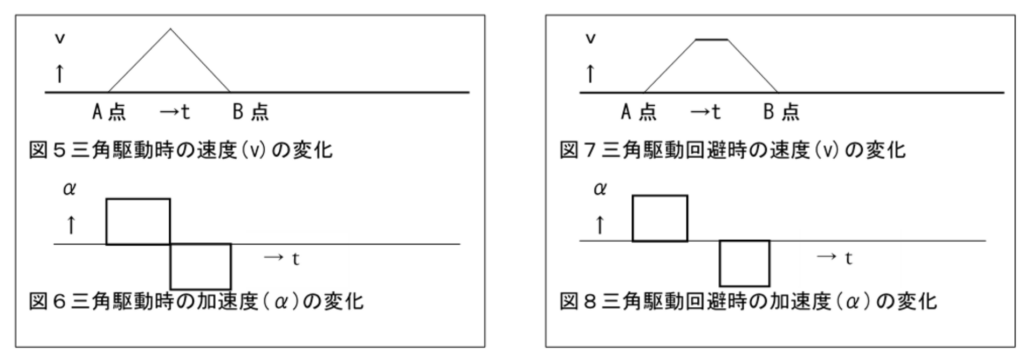
この機能を用いる事で三角駆動による弊害を回避することができます。 この機能により、図8の様に加速度の
変化量(加速からいきなり減速する)が抑えられています。 弊社のモーションコントローラは標準で、
この<三角駆動防止機能>を有していて、ユーザ様が任意で有効・無効を選択はもちろん台形<平らな部分>部分を
任意で設定が可能です。
ただし、実はこれには欠点があります、台形部分を意図的に作るということは。
速度を抑えているのでその分位置決めに要する時間は伸びてしますが振動の抑制と位置決め時間の良いとこ取りができる様に設定を調整できる仕様になっています。
※1.自起動周波数:ステッピング・モータが脱調せずに起動(動作)出来る周波数(速度)の事を言います。しかし、
脱調しない速度での周波数を高速で使用すると振動や衝撃は大きくなりますので速度の選定には注意が
必要です。
※2.脱調状態:ステッピング・モータは入力指令(パスル指令等)に同期して動作(回転)します。
しかし、急激な速度変化や負荷変動があると入力指令に同期出来なくなり、モータが停止状態や正常に回転しなく
なるステッピング・モータ特有の状態(現象)を言います。
※補足.ハンチング:これもステッピング・モータ特有の状態(現象)ですが、比較的遅い回転数で共振状態を起こし大きな
振動となったり、停止(脱調)したりします。 使用するステッピング・モータの種類やその負荷の状態によって変り
ますのでご使用になる状態で確認するようにして下さい。 通常は共振状態を起こす領域(回転数)を使用せず
適切な加速・減速時間を設定し共振状態を起こす領域を回避して使用します。
3.曲線駆動
先ほどお話した台形駆動・三角駆動の様な直線的な加速・減速でなく、曲線的な加速・減速を行うことで一層スムーズなモーションコントロールの実現が可能です。特にステッピング・モータには有効です。
加速・減速の変化率を一定ではなく曲線的な変化率で行います、これらにはいろいろな方法がありますが弊社のモーションコントローラでは次に述べる「サイクロイド曲線」と「変形台形曲線・変形正弦曲線」を選択して頂く事が出来ます。
3-1 サイクロイド曲線
サイクロイドとは、円がある規則にしたがって回転するときの円の上のある点(定点P)が描く 軌跡(青色)でえられる
曲線の総称を言います。
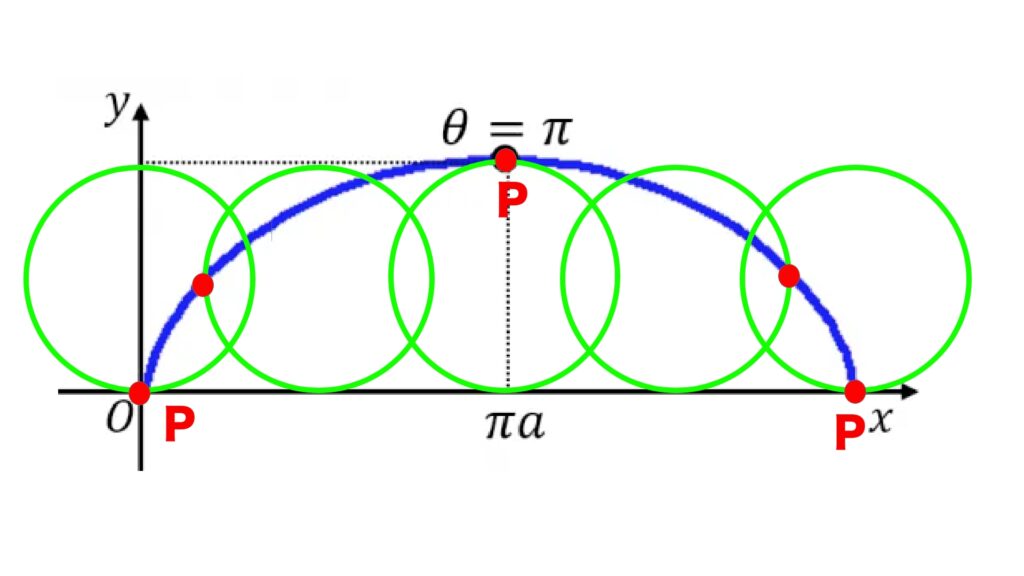
弊社のサイクロイド曲線は式1で演算されます。
・・・・式1
f:周波数 F:最大周波数
t:経過時間 T:最大周波数に達する時間
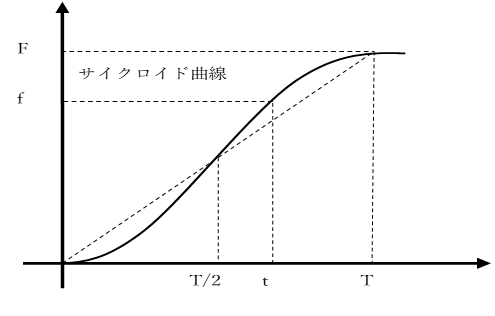
加速度が最大となりすますので、場合によってはそれが振動・衝撃などの不都合の要因となる事 もあります。
3-2 カム曲線(変形台形曲線、変形正弦曲線)
変形台形曲線・変形正弦曲線を弊社のモーションコントローラで採用しています。 カム曲線の種類の中でも良く利用されている方式でサイクロイド曲線に比べ最大加速度(図9のT/2付近)が軽減され、より滑らかな動作を実現しています。
〇変形台形曲線
最大加速度の変位を小さくするために開発された標準的な曲線駆動の方式で、高速・軽加重向きのカム曲線です。
〇変形正弦曲線
カム機構に多く採用されている曲線で中速・中過重の一般向きといわれています。バランスの
良い使い易い曲線です。
【一口メモ】

その際の演算は三角関数等を用いるのですが、最近のパソコンの様に高性能な処理能力を持ったマシンであれば問題無いでしょうが、通常我々の様な産業機器で使用しているCPUで三角関数の処理を多用するとその演算処理に多くのパワーを要してしまい他の処理に影響がでてしまいますので、弊社では独自の手法で曲線駆動を実現する事でスリム化(コストダウン)を払って、滑らかな動作(モーションコントロール)を実現しています。
以下は変形台形曲線・変形正弦曲線の弊社コントローラの取扱説明書からの抜粋内容です、
ご参考までに。
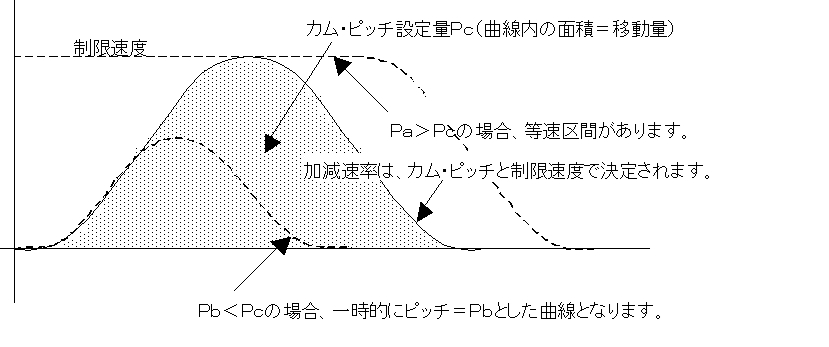
位置決め量とカム・ピッチ(Pc)が等しい場合には、制限速度まで加速する加速・減速対称のカム曲線が得られます。
位置決め量がカム・ピッチより大きい場合(Pa)、(Pa-Pc)相当の等速区間ができます。
位置決め量がカム・ピッチに満たない場合(Pb)、一時的にカム・ピッチ=Pbとした曲線で移動します。この場合の制限速度は最大加速率が(Pc)の場合と等しくなるように決定されます。
変形台形、正弦曲線の加減速率はカム・ピッチと制限速度により決まります。
*カム・ピッチ(Pc)はパラメータで設定します。
このほかに以下のカム曲線も有りますのでご参考までに紹介いたします。
〇単弦曲線
一般的には等速度曲線といわれているものです、ハーモニックまたはアルキメデスとも呼ばれています。
〇変形等速度曲線
位置決め動作中の一定区間を等速で行うときに使用するカム曲線です。
〇トラペクロイド曲線
停止エネルギーを緩和するために減速のカム割り付け角を大きくした曲線です。
東阪電子の技術情報
弊社のモーションコントール製品は、各種加減速手法の対応はもちろんお客様の要望に応じた設計・開発・製造についてもお気軽にご相談下さい。
