
中学の理科の授業で教わったと思いますが、覚えていますでしょうか。
I=V÷R では表される電気回路では良く使われる 電流・電圧・抵抗 の関係についての法則です。
オームの法則とは(入門編)
導電現象にて電気回路の部分に流れる電流とその両端の関係を示す法則のことです。クーロンの法則とともに電気工学では重要な法則のひとつです。
1781年にヘンリー・キャヴェンディッシュ氏によって発見されてましたが、そのことは彼の死後数十年経過後の1879年にその遺稿を纏めたイギリス・スコットランドの理論物理学者のマックウエル氏寄って「ヘンリー・キャヴェンディシュ電気学論文集』として出版されるまでは世間には未公表であったため世間には知られていませんでした。1826年にドイツの物理学者のゲオルグ・ジーモン・オーム氏によって発見・公表されたので彼の名前からオームの法則と呼ばれる様になりました。
(*)導電現象:電線、電気抵抗などに電流が流れる現象の事を言います
(*)クーロンの法則:荷電粒子間に働く反発、または引き合う力がそれぞれの電荷の積に比例し、距離の2乗に反比例すること(逆2乗の法則)を示した電磁気学の基本法則。
オームの法則とは 【電流は電圧に比例する】 という法則です。
例えば、抵抗値が5Ωで一定とした場合そこに流れる電流は抵抗に印加される電圧に比します。
I=V÷R ・・電流【I】は抵抗【R】が一定であれば、電圧【V】が増えれば増えます。
電流【I】は電圧【V】が一定であれば、抵抗【R】が増えれば減ります。
V=IxR ・・電圧【V】は抵抗【R】が一定であれば、電流【I】が増えれば増えます。
電圧【V】は電流【I】が一定であれば、抵抗【R】が増えれば増えます。
R=V÷I ・・抵抗【R】は電流【I】が一定であれば、電圧【V】が増えれば増えます。
抵抗【R】は電圧【V】が一定であれば、電流【I】が増えれば減ります。
上記の様に 電流【I】・電圧【V】・抵抗【Ω】の3つのうち2つがわかっていれば、残りの1つを求める(計算)することができる法則になります。
電流を求める時はどうすればよいでしょうか
文頭でI=V÷R と書きましたがこれは
電流【I】=電圧【V】÷ 抵抗【R】
で求める事が出来ます。
電気の基本ですので覚えておくと便利です。
電圧[V]・電流[I]・抵抗[R]それぞれには[単位]と「よみ」があります。
電圧: 表記は[V]で単位は「V:ボルト」です([E]と表記する場合もあります)
電流: 表記は[I]で単位は「A:アンペア」です
抵抗: 表記は[R]で単位は「Ω:オーム」です
・練習問題①
電流I(A)を求めましょう
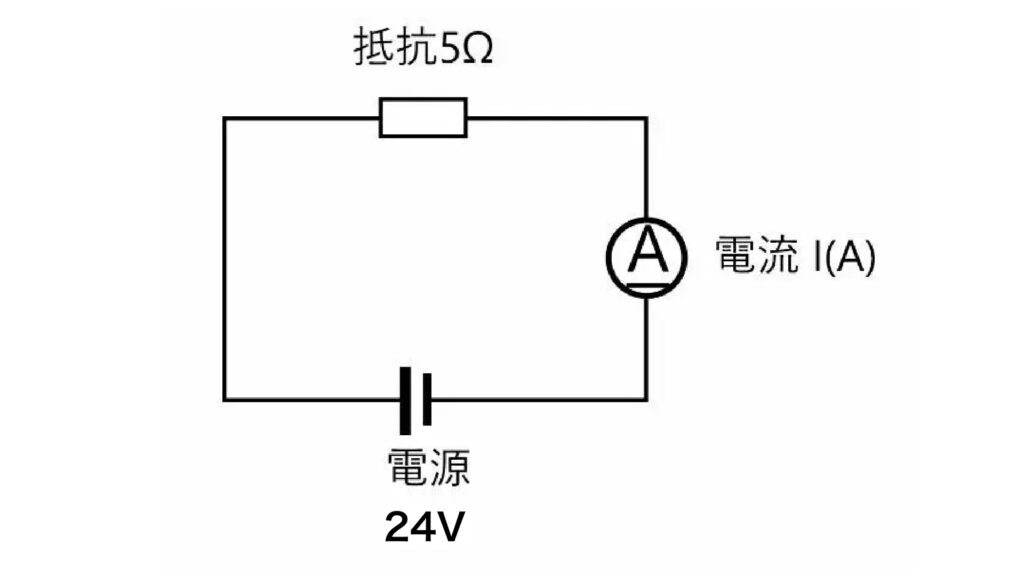
電流【I】=電圧【V】÷ 抵抗【R】 で求められますので。
24(V) ÷ 5(Ω) = 4.8(A)
電流【I】は4.8(A)となります。
抵抗を求めるときはどうすればよいでしょうか。
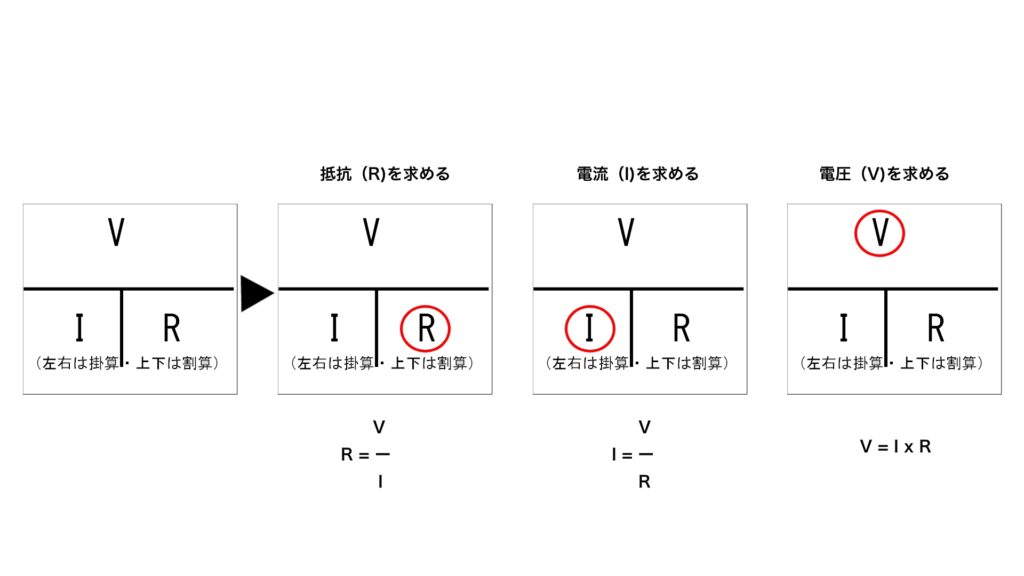
簡単で便利な方法があります、上の図で求めたい箇所を隠してください。(赤丸印)
(左右は掛算 上下は割算 で計算します)
・抵抗は同様に 図の 「R」 を隠して下さい。
V/I =>V÷I => 抵抗【R】=電圧【V】 ÷ 電流【I】
です。
・練習問題②
抵抗R(Ω)を求めましょう
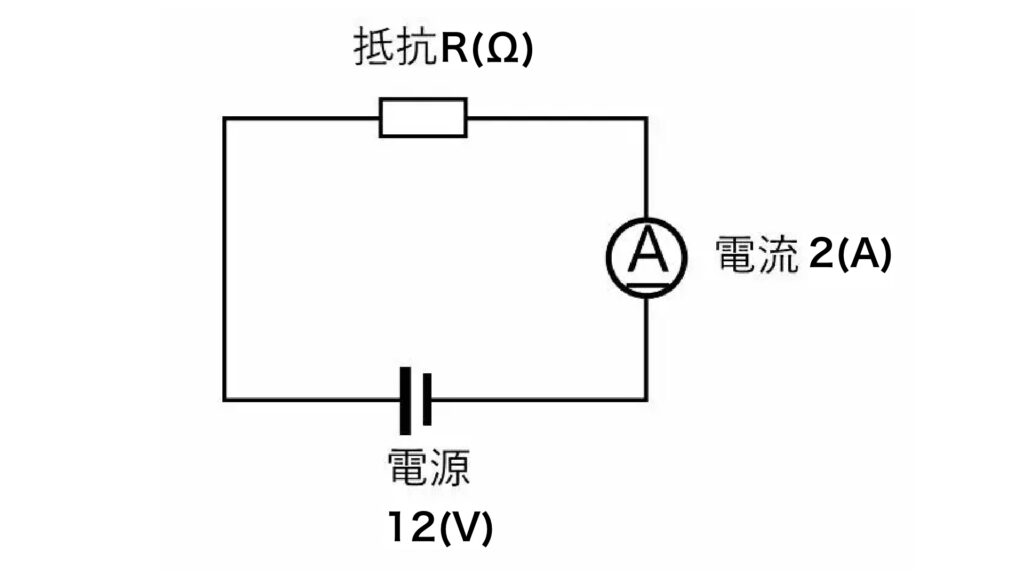
抵抗【R】=電圧【V】 ÷ 電流【I】で求められますので。
12(V) ÷ 2(A) = 6(Ω)
抵抗【R】は6(Ω)となります。
電圧を求めいたい時はどうすればよいでしょうか
電圧を求めたい場合は「V」をかくすと
I・R =>IxR => 電圧【V】=電流【I】 x 抵抗【R】
です。
・練習問題③
電圧V(V)を求めましょう
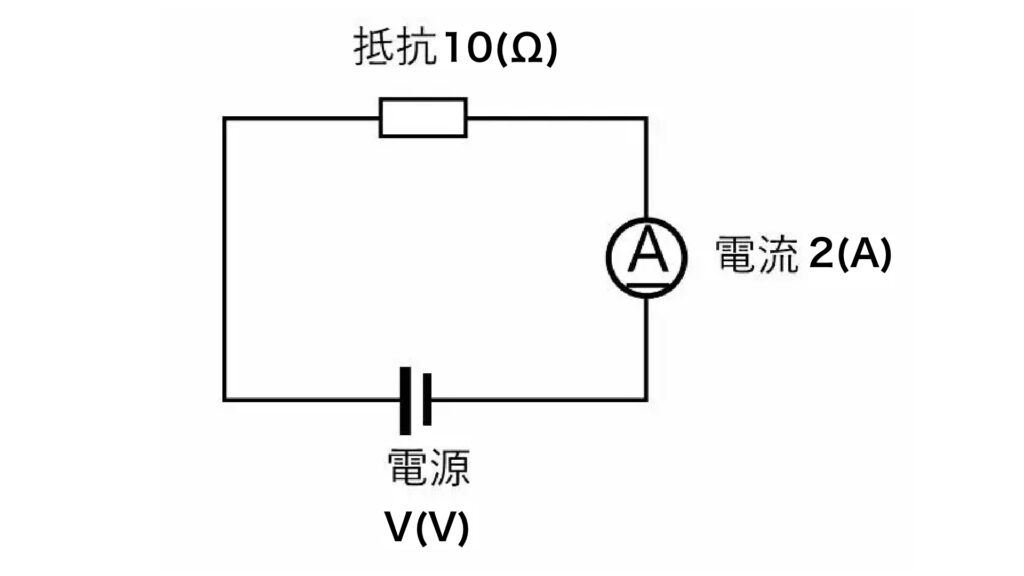
電圧【V】=電流【I】 x 抵抗【R】で求められますので。
2(A) x 10(Ω) = 20(V)
電圧【V】は20(V)となります。
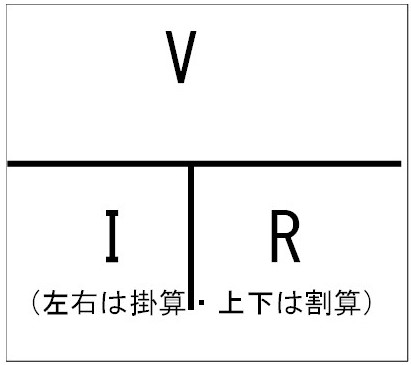
如何でしたでしょうか、この図だけ覚えておくと便利かと思います。
これでオームの法則の入門編は完璧ですね。
素子の合成計算(応用編)
直列接続と並列接続とで電圧・抵抗・電流の計算方法が違います。抵抗が複数ある場合一見複雑に見えますが、一つずつ処理していけば良いです。
抵抗が複数ある場合(直列に接続の場合)
・練習問題④
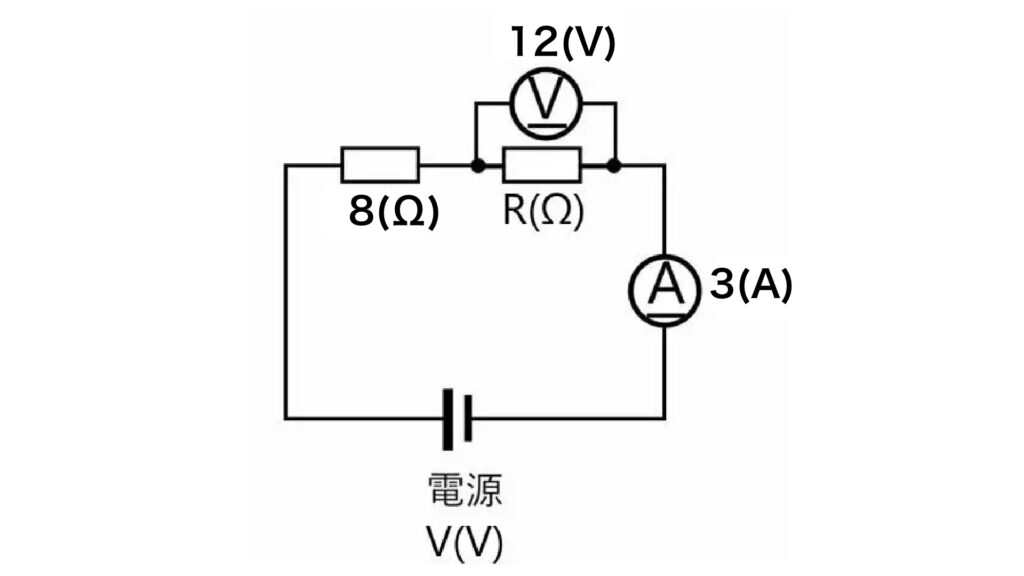
この回路での
①R(Ω)の抵抗値
②電源V(V)の電圧
を求めましょう。
<ヒント>
・抵抗が2つありますが、左側の【8Ω】の抵抗と右側の【RΩ】に流れる電流は同じです。
この場合は3(A)となります。
・左側の【8Ω】の抵抗の両端の電圧と右側の【RΩ】の両端の電圧(12V)の合計が電源V(V)になります。
①R(Ω)の抵抗値の計算は次の通りになります
・抵抗R(Ω)に流れる電流は3(A)かつ抵抗R(Ω)の両端の電圧は12(V)ですので。
抵抗は
抵抗【R】=電圧【V】 ÷ 電流【I】で求められますので。
12(V) ÷ 3(A) = 4(Ω)
抵抗【R】は4(Ω)となります。
②電源V(V)の電圧の計算は次の通りになります
・左側の【8Ω】の抵抗の両端の電圧と右側の【RΩ】の両端の電圧(12V)の合計が電源V(V)ですので抵抗8(Ω)の両端の電圧を求めるには
電圧【V】=電流【I】 x 抵抗【R】で求められますので。
3(A) x 8(Ω) = 24(V)
抵抗8(Ω)の両端の電圧は 24(V) となりますので
電源V(V)は
24(V) + 12(V) = 36(V)
となります。
・ここで別の考え方もあります。左側の抵抗8(Ω)と右側の抵抗R(Ω)を一つの抵抗として考えてみましょう。
右側の抵抗R(Ω)は先ほど 4(Ω)と求められましたので。
直列の抵抗は 8(Ω) + 4(Ω) = 12(Ω) として一つの抵抗として考えてみると。
電圧【V】=電流【I】 x 抵抗【R】で求められますので。
3(A) x 12(Ω) = 36(V) となりますので
電源V(V)は
24(V) + 12(V) = 36(V)
となります。
抵抗が複数ある場合(並列に接続の場合)
・練習問題⑤
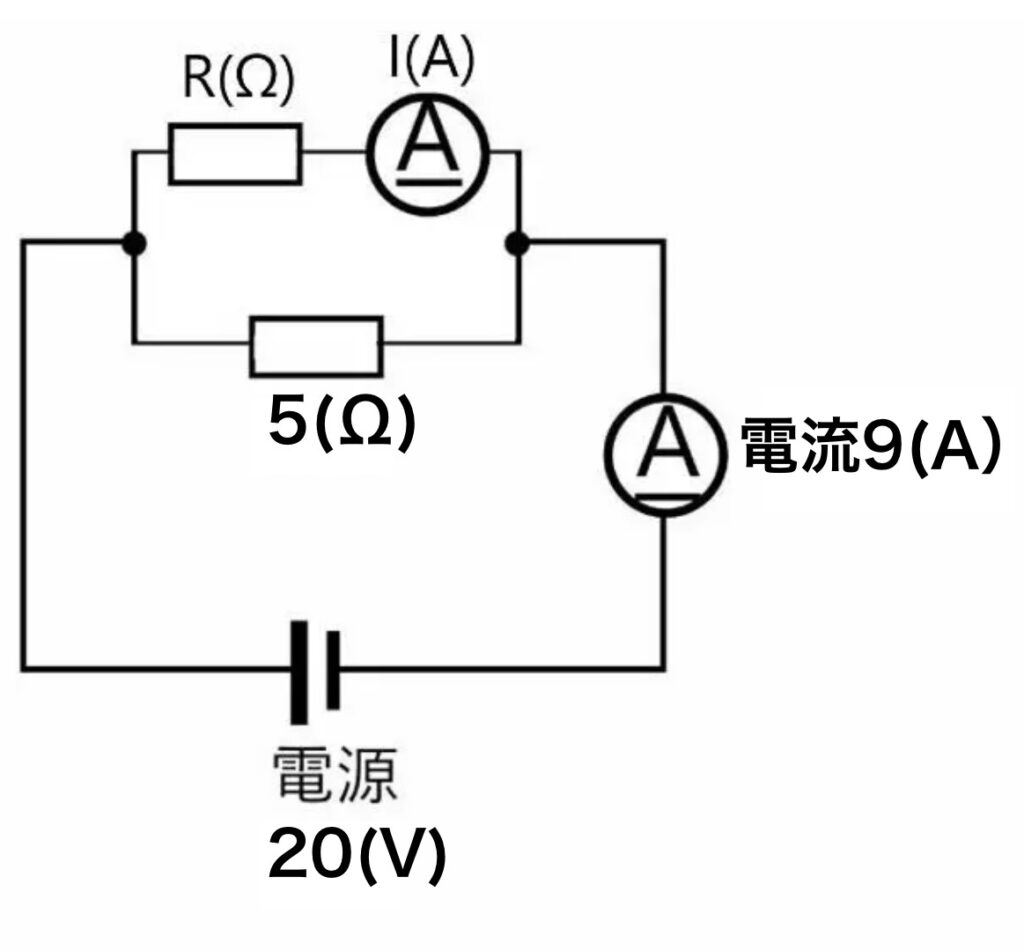
この回路での
①抵抗Rに流れる電流I(A)の電流値
②R(Ω)の抵抗値
を求めてみましょう。
<ヒント>
・抵抗R(Ω)に流れる電流I(A)と5(Ω)に流れる電流の和(足し算)は電流9(A)になります。
・抵抗R(Ω)と抵抗5(Ω)の両端の電圧は同じで、電源20(V)になります。
①I(A)の電流値
5(Ω)に流れる電流を計算します。
5(Ω)の両端の電圧は20(V)ですので。
電流【I】=電圧【V】÷ 抵抗【R】 で求められますので。
20(V) ÷ 5(Ω) = 4(A)
です。
・抵抗R(Ω)に流れる電流I(A)と5(Ω)に流れる電流の和(足し算)は電流9(A)になりますので
I(A) = 9(A) - 4(A)
I(A)の電流値は5(A)となります。
②R(Ω)の抵抗値
・抵抗R(Ω)と抵抗5(Ω)の両端の電圧は同じですので
抵抗【R】=電圧【V】 ÷ 電流【I】で求められますので。
20(V) ÷ 5(A) = 4(Ω)
R(Ω)の抵抗値は4(Ω)となります。
おまけ(並列抵抗の計算方法)
直列接続の場合は単純に足し算で求める事が出来ますが、並列接続抵抗の場合の計算は
練習問題④の直列接続の抵抗の時の様に足し算で計算する事は出来ません。
練習問題⑤の並列接続の抵抗を一つの抵抗として考える事ができます。
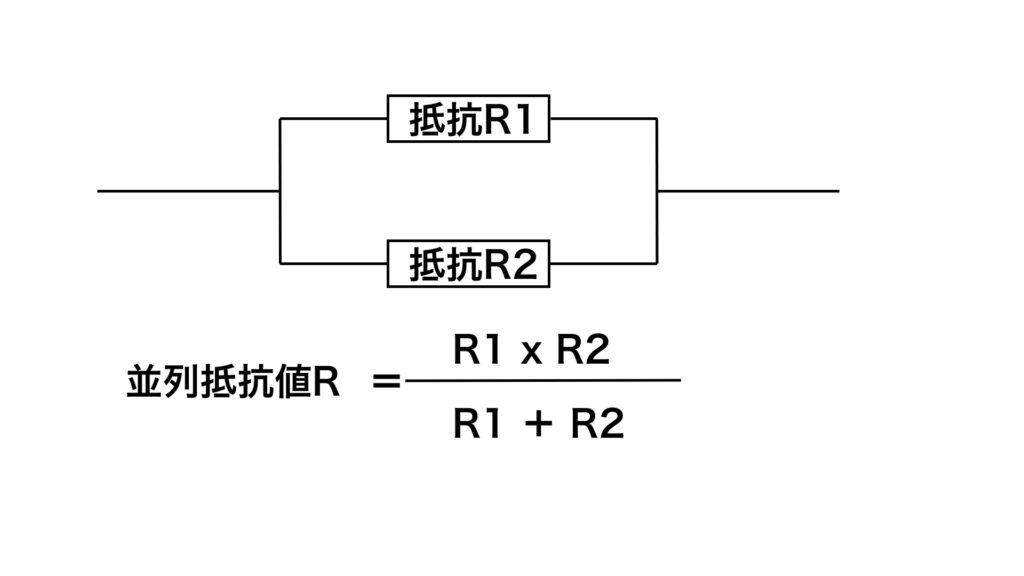
図の様な並列抵抗の場合はこの様な計算式になります。
数学的に言いますと<逆数の和の逆数>です、それを整理すると上の式になります。
練習問題⑤をこの計算式で計算すると
4(Ω) x 5(Ω) 20(Ω)
並列抵抗値 = ―――――――――― = ――――= 2.222222 (Ω)
4(Ω) + 5(Ω) 9(Ω)
約2.22(Ω)になります。
・このように電気の分野ではオームの法則を用いる事で、いろいろな電気の現象が計算によって求める事ができます。基本的な公式を覚えやすい方法で理解をして、直列接続・並列接続特有を理解していれば、今回より複雑な場合の計算も求める事がきっと出来ます。
技術的な掘り下げ

高周波回路における課題
オームの法則は抵抗値が一定である理想的な線形回路を前提としています。しかし実際の回路では高周波信号を取り扱う場合があり少し複雑な要素が発生します。
① 高周波におけるインピーダンスの概念
インピーダンス(Z)は単なる(R)に加えリアクタンス(X)を含む複素数で表されます。リアクタンスは回路内の(インダクタンス)やコンデンサ(キャパシタンス)による電流と電圧の位相差が生じます。
Z=R+jX
ここで jは虚数単位 Xは次の様に計算されます。
・インダクタンス(L)
XL=2πfL
f:周波数
L:インダクタンス値
インダクタンスは周波数が高くなるとリアクタンス値は大きくなります。
・キャパシタンス(C)
XC=1÷(2πfC)
C:コンデンサ容量
キャパシタンスは周波数が高くなるとリアクタンス値は小さくなります。
② 高周波回路での応用
・インピーダンスマッチング:
通信回路やアンテナ設計では、通信側と受信側のインピーダンスを一致させることで信号反射を最小化にすることでエネルギー伝達効率を高めます。
・スキン効果:
高周波信号では電流が導体の表面に集中する「スキン効果」が発生します。この現象により有効面積が減少して抵抗が増加します。(本章で説明したオームの法則が単純に適用されない場合が発生します)スキン効果を緩和するために、リッツ線(細い導線を束ねたもの)や表面処理技術が用いられます。
・信号損失:
高周波信号が伝送線路を通過する際損失が発生します。この損失は主に導体の抵抗と誘導体の損失(材料内部のエネルギー損失)に起因します。適切な材料選定や設計が重要となります。
シミュレーション技術
現在の電子機器設計では物理的な試作前に回路やシステム全体をシミュレーションすることが一般的になって来ています。シミュレーション技術は、オームの法則を基本にして複雑な電気的振る舞いを予測します。
・SPICEシミュレーション:
SPICE(Simulation Program with Integrated Circuit Emphasis)はアナログ電子回路のシミュレーヨンに特化したツールです。SPIDEでできることは次の事になります。
① DC解析:
定常状態での回路の動作を評価。各部品の電圧や電流分布を計算します。
② AC解析
小信号周波数応答を評価。フィルタ回路や増幅回路の周波数特性を確認します。
③ トランジョット解析
過渡応答(時間変化)を評価。スイッチング回路やデジタル回路での瞬時応答を確認することができます。
・システムレベルのシミュレーション
SPICE以外にもシステム全体の挙動をシミュレーションできるものもあります。
材料科学との関連性
オームの法則は導体や半導体・絶縁体などの材料特性とも密接に関係しています。
・導体の抵抗率と温度依存性
材料の抵抗率(ρ)は温度に応じて変化します。金属の場合温度が上昇すると抵抗率が増加します。これは電子が原子の熱振動に影響されやすくなるためです。
ρ(T)=ρ0(1+αT) の式で表されます。
ρ:温度がT℃の時の抵抗率
ρ0:温度が0℃の時の抵抗率
α:温度係数
T:温度℃
・半導体材料の抵抗特性
半導体ではキャリア密度(自由電子や正孔の数)が温度や外部刺激(光、電界など)によって大きく変化します。これらによって抵抗値は非線形に変化します。
3-4 非線形性と限界
オームの法則は線形を前提としていますが、現実の回路部品の多くは非線形特性を持っています。
例:
ダイオード:順方向電圧が一定値を超えると急激に電流が流れます。
トランジスタ:電流の制御に基づく非線形増幅特性を持ちます。
・回路動作の複雑化:
非線形部品を含む回路では電流と電圧の関係が複雑化します。このような場合線形モデルではなく数値シミュレーションや実機での検証が不可欠となります。
・分布定数回路の課題:
高周波回路や長い伝送経路では抵抗・インダクタンス・キャパシタンスが分布的に存在するために、オームの法則を直接適用できません。分布定数回路理論(波動方程式や反射係数)が適用されます。
