2進数と16進数は、コンピューターやデジタルエレクトロニクスの世界でよく使われる数値表現の形式です。
1.概要
これらの数の表現方法は、次のような用途で使用されます:
①コンピュータープログラミング:
コンピューターでは基本的に2進数を使って情報を処理しますが、プログラミングの際には16進数を使ってより簡潔に値を表現することがあります。特にメモリアドレスやビットフラグなどの場合に便利です。
②デジタル回路設計:
コンピューター内部の回路は2進数で表現されます。論理ゲートやデジタルICの設計などにおいて、2進数が使われます。
③ネットワーク:
IPアドレスなど、ネットワーク関連の情報は一般的に16進数で表示されることがあります。
④データ通信:
データ通信のパケットやバイト列などは、16進数表示されることがあります。
⑤データベース:
データベースの管理やバックアップの際に、2進数や16進数でデータをエクスポート・インポートする場合があります。

2.16進数と2進数について
普段我々が普段よく使っているのは10進数です。まずは10進数について考えてみましょう。
10進数では0~9の10個の数を用いて10進数が表されます。
0,1,2,3,4,5,6,7,8,9まで10個数えたら桁が繰り上がって10からかぞえます、それを繰り返していきます。
・16進数(Hexadecimal)は、0から9までの数字とAからFまでの6つのアルファベットを用いて表現される数の体系です。
0,1,2,3,4,5,6,7,8,9、A、B、C、D、E、Fまで16個数えたら繰り上がります。10進数と同じ「10」では混同しますので16進数では「0x10」と表します。 「0x」が16進数の事と理解しましょう。
例えば、10進数での10は16進数ではA、15はFと表現されます。16進数は、長い2進数の数を短く表現することができるため、コンピューターのプログラムやメモリのアドレス、色の表現などによく使われます。
・2進数(Binary)は、0と1の2つの数字だけを使って表現される数の体系です。これはコンピューター内部の情報を扱うのに最も基本的な表現方法であり、デジタル情報を記述するのに必要不可欠です。コンピューターは実際には2進数を用いて情報を処理し、16進数や10進数への変換を行って人間に表示されます。
2進数は「10010」と1と0のみで表しますが、「10010b」と表します
これで10進数・16進数と区別がつきますね。
「0x10010」 は16進数
「10010b」は2進数
「10010」 は10進数(10進数はなにもつけませんが 10010dとする場合もありますが一般的に10進が日常生活で使っていて d はつけませんね。)
です。

3.16進数と2進数の表し方
3-1 16進数の表し方
16進数は、0から9までの数字とAからFまでのアルファベットを用いて表現される数値の体系です。10進数と同じく基数が16であるため、10進数の10以上の数字を一つの記号で表現することができます。
具体的な表現方法は以下のようになります。
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
これらの記号を組み合わせることで、16進数の数値を表現します。例えば、10進数
の数値と対応する16進数の表現は以下のようになります。
• 10進数の0は16進数で”0x0″となります。
• 10進数の1は16進数で”0x1″となります。
• 10進数の9は16進数で”0x9″となります。
• 10進数の10は16進数で”0xA”となります。
• 10進数の15は16進数で”0xF”となります。
• 10進数の16は16進数で”0x10″となります。
• 10進数の255は16進数で”0xFF”となります。
• 10進数の256は16進数で”0x100″となります。
このように、16進数では10進数よりも一つの記号で大きな数を表現することができ
ます。主にコンピューターやプログラミングにおいて、2進数との変換やメモリアド
レスなどを表現する際に使用されます。
3-2 2進数の表し方
2進数は、0と1の2つの数字だけを使って数値を表現する方法です。
具体的に2進数の表記方法を説明します。
• 10進数の0は2進数で “0000 0000b”となります。
• 10進数の1は2進数で “0000 0001b”となります。
• 10進数の9は2進数で “0000 1001b”となります。
• 10進数の10は2進数で “0000 1010b”となります。
• 10進数の15は2進数で “0000 1111b”となります。
• 10進数の16は2進数で “0001 0000b”となります。
• 10進数の255は2進数で “1111 1111b”となります。
• 10進数の256は2進数で”1 0000 0000b”となります。
*2進数の場合0 1 のみの表記なので 上記の様に4ビット(又は8ビット)毎で区切って記載する事が多いです。
10進の256を2進数で”100000000b”の表記ではわかりにくいですね。
最新のパソコンに使用しているCPUは64Bitですので、2進数で表記すると”0” “1”が 64個になります。
4.2進数・16進・10進数の各々の変換の方法
少し数学的になります。
4-1 2進数を10進数へ変換
2進数の下位から 2の0乗、2の1乗、・・・・2のn乗となりますのでそれに”1”又は“0” を掛け算します。
例えば、「1100 1001」を10進数に変換してみましょう。
(2の7乗)x1 + (2の6乗)x1 + (2の5乗)x0 + (2の4乗)x0 + (2の3乗)x1 + (2の2乗)x0 + (2の1乗)x0 + (2の0乗)x1
を計算しますと
128+64+0+0+8+0+0+1=201 と なります。
2進数「1100 1001」 は 10進数「201」 となります。
4-2 10進数を2進数へ変換
同じ様に10進数「201」を2進数に変換してみましょう。
方法は:10進数を「2」で割って、その商が1になるまで割り算を繰り返していきます。その余を最後から順番に並べると2進数に変換できます。
10進数 余り
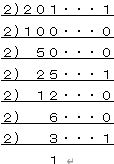
となって下から順番に並べますと「1100 1001」となります。
このように計算を行えば、何桁の10進数でも容易に2進数へ変換が出来ます。
4-3 2進数から16進数への変換
2進数を16進数で表すには、前項のとおり2進数の下位から4ビットずつ区切って、その4ビットを16進数で表します。つまり、2進数を4ビット束ねると、「0000~1111」で(2の4乗)=16通りの並び方がありますので16進数が用いられている様です。
そして、束ねた4ビットを10進数に変換して、さらにそれを16進数に変換します。先ほどの例と同様に「1100 1001」を16進数に変換してみましょう。
(2の3乗)x1 + (2の2乗)x1 + (2の1乗)x0 + (2の0乗)x0 = 12
(2の3乗)x1 + (2の2乗)x0 + (2の1乗)x0 + (2の0乗)x1 = 9
となり10進数の12と9は、16進数では「C」と「9」になります。
したがって、2進数「1100 1001」は16進数「C9」となります。
4-4 16進数から2進数への変換
16進数の「C9」を2進数へ変換してみましょう。
今まで説明致しました事(工程)を逆に実行するとできます。まず16進数を10進数に変換し、10進数から2進数に変換します。
ですから、16進数の「C」と「9」は10進数ではそれぞれ「12」と「9」になります。次にそれぞれを2進数に変換すると「1100」「1001」となります。最後に各々を統合しますと 16進数の「C9」は2進数では「1100 1001」となります。

4-5 10進数から16進数への変換
10進数から2進数への変換と同様に、10進数を「16」で割り、その商が15以下になるまで割って行きます。その余りを最後から順番に並べると、16進数に変換することができます。
10進数201を16進数に変換してみましょう。
10進数 余り
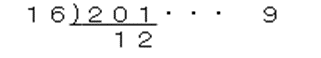
下から順に並べますと。
12(C)・9となります。
10進数「201」は16進数「C9」となります。
4-6 16進数から10進数への変換
16進数の「C9」を10進数へ変換してみましょう。
2進数の時と同様のやり方で変換ができます。
16進数の下位から、16の0乗、16の1乗、16の2乗、16の3乗・・・を掛けて
(16の0乗x9)+( 16の1乗xC)
を計算します。
(1×9)+(16×12)=9+192=201 となります。
ご紹介した方法は一般的な方法になります、これらの他にも様々な計算方法があるかと思われます。最近では電卓を使用されているかとおもいますが、変換の理屈(理論)を理解されるのも良いかと思います。
