FPUとはコンピュータ(PC)の(演算)処理装置の一部で、数値データの浮動小数点の計算に特化したIC(演算装置)です。
1.浮動小数点とは
浮動小数点は小数点以下を任意で設定でき(一定の制限はあります)、処理できる数値の範囲が広くなることによりグラフィック処理・シミュレーション・科学計算などでよく用いられます。 浮動小数点方式においては、固定長の仮数部と固定長の指数部の2つの部分の組み合わせによって、数値を表現します。コンピュータの数値表現においては浮動小数点方式が多用されます
浮動小数点とは、普通の方が想像されるような小数点ではなく、計算で誤差が発生することを前提と考える数値データの事を言います。
言い換えると、浮動小数点を扱う時は常に近似値計算である事を意識してその結果の精度を考えて計算を行う必要があります。
浮動小数点の逆は固定小数点というものがあります。通常使っている整数のデータがこれに当たります。整数ですので、必ず1刻みですので誤差は出ませんが扱える数値の範囲が広くありません。
※64bit整数だと、-9,223,372,036,854,775,808~9,223,372,036,854,775,807の範囲となり、10進数で19桁になります。
それに対して、浮動小数点は誤差が発生しますが広い範囲の数値を扱えます。ほとんど0に近いナノレベルの数値から宇宙規模の大きな数値まで対応が可能です。
1-1 浮動小数点は計算式の桁数を抑える事ができる
コンピュータで数字の演算を行う場合、整数演算と小数演算の2つに分けて実装するのが普通です。これは「何桁まで処理する必要があるか」というニーズが根本的に違うためです。
整数の場合、普通(なにを基準に普通というかは置いておくとして)は10桁くらいの計算ができれば十分と思われます。もちろん企業における会計処理などでは10桁では足りません(売上1兆円を表現するのには12桁が必要です)が、そういう規模の大きな処理はちょっと置いておくとして、9桁か10桁あれば大体用が足ります。
ところが小数の場合、そもそも何桁まで処理できれば足りるか、というのはあまりに多種多様です。例えば利息の計算の場合、100万(これで7桁必要です)に利子が数銭(これが2桁)だから9桁でギリ。1000万くらいの定期預金では10桁以上が必須になる。
ただしこれだと整数部8桁+小数部2桁だが、なかには整数は2桁程度で良いけど小数が5桁ほしいというニーズもあります、両方に対応しようとすると13桁くらいないと足りなくなります。実際はもっと桁数が必要になるケースもあるかと思われます。
これでは効率が悪いので、小数を扱う場合には浮動小数点と呼ばれる方式を採用することになった。例えば123456.789という数字を扱う場合、以下の様にデータが保存されます。

※123456.789の場合
固定小数点の場合:123456.789 整数部6桁+小数部3桁
浮動小数点の場合:1.23456789×105 仮数部9桁+指数部1桁
ここで、元の数値が12345678.9や1.23456789だった場合を考えるとわかりやすいかと思います,次の様になります。
※12345678.9の場合
固定小数点方式:12345678.9 整数部8桁+小数部1桁
浮動小数点方式:1.23456789×108 仮数部9桁+指数部1桁
※1.23456789の場合
固定小数点方式:1.23456789 整数部1桁+小数部8桁
浮動小数点方式:1.23456789×100 仮数部9桁+指数部1桁
このように固定小数点方式では1.23456789~12345678.9までのすべての数字を扱うためには整数部8桁+小数部8桁が必要となります。
これに対して浮動小数点方式では常に仮数部(1.23456789を格納するところ)が9桁+指数部(10のべき乗の値を格納するところ)の1桁で、合計10桁で済みます。
使用する値の範囲がきっちりと決まっていて、そこからはみ出さないという場合なら固定小数点方式でも不利はありません(むしろ便利かもしれません)が、どんな値がくるか予想がつかない場合では、浮動小数点を利用したほうが、格納エリアを小さく抑えられることになります。
1-2 浮動小数点の表現(精度)
1980年代頃まではこの浮動小数点の方式には標準が有りませんでした、コンピューターメーカーがおのおの都合でフォーマットを決めていたました、1985年にIEEE(米国電気電子学会)がIEEE 754と呼ばれる標準規格(IEEE 754-1985)を定めて、各社もこれに順ずる形で実装するようになりました。したがって最近はよほど変な要求がない限り、浮動小数点のフォーマットは共通になっています。
ちなみにそのIEEE 754であるが、その後2008年にも改定されており(IEEE 754-2008)、いろいろ表現が増えている。昨今のCPUはすべてこのIEEE 754-2008に準じた演算をしていると考えていい様です。
IEEE 754-2008を簡単に説明いたします。IEEE 754-2008では、数字の表現について次の8つのフォーマットが定められています。
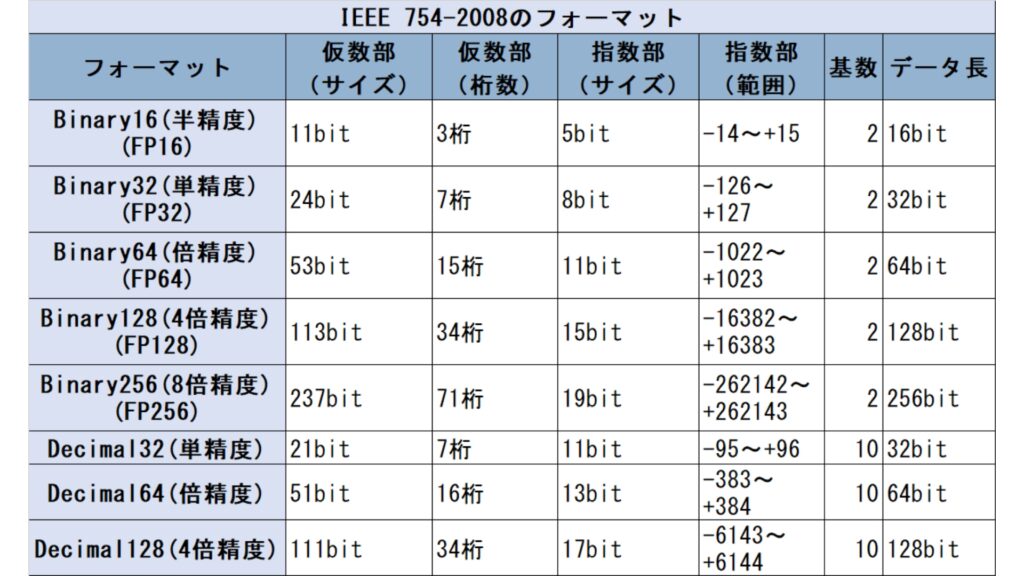
ただしこのうちBinary16/Binary256/Decimal32の3つのフォーマットに付きましては交換用と定められています。交換用とはデータの受け渡しをするためのもので、たとえばBinary16ならBinary32/64/128との間で相互変換ができれば良く、演算そのものを実装することは行いません。実際には昨今AIに絡んで、Binary16の演算を実装している例が多くなっています。
2.FPU(浮動小数点ユニット)とは
2-1 FPUの概要
FPUは浮動小数点を高速に処理する事を得意とした集積回路(IC)でコンピュータ(PC)のCPUの数値演算処理の肩代わりをする事で使用します。
以前はコンピュータ(PC)の拡張カードやCPUの拡張バスとして専用のソケットを装着して使用していました。これはかつての安価なコンピュータ(PC)では大量の浮動小数点演算を行う用途は限られていたため、FPUが拡張装置としてCPU本体とは別に存在していた為です。
しかし近年ではCPUの機能・性能の向上やコンピュータの使用用途が拡大し、FPUの役目をする演算機能をCPU内部に盛り込まれる様になり、一般的なコンピュータ(PC)にも使用される様になりました。
2-2 FPUの方式
・I/Oプロセッサー形式
FPUをI/Oポートに接続して、通常の周辺機器と同様にI/Oポートを介してデータのやり取りを行なう形式。FPUは周辺機器として扱われるので、CPUと同じメーカのFPUを使わなくてもよく、8ビットCPUの時代には、当時高額だったAm9511などの代わりに別メーカの電卓用CPUをI/Oポートに接続して使うことで一部のユーザで実験的に行なわれた方式です。
(*) Am9511:8ビット時代の高速浮動小数点演算ユニットの事です。
・コプロセッサ方式
CPUとFPUがアドレスバスとデータバスを共有し、一体化して動作する方式です。ユーザ側から見るとCPUの命令が拡張されたように見える方式です。
・乗っ取り方式
コプロセッサ方式の発展形です。コプロセッサが実際にはCPUとしての全機能を受け持っており、制御は完全にコプロセッサ側に渡してしまい、既存のCPUは機能を停止させる方式です。
2-3現在では
現在ではFPUはプロセッサーに内蔵されるようになり、FPUはスーパースカラーで他ユニットと並列動作させることができるなど様々なメリットがあるため、現在ではFPUを単体で用いることは珍しくなっています。
(*)スーパースカラー:プロセッサーのマイクロアーキテクチャにおける用語です、複数の命令を同時にフェッチし、複数の同種のあるいは異種の実行ユニットを並列に動作させ、プログラムの持つ命令レベルの並列性を利用して性能の向上を図るアーキテクチャです。
簡単に言いますと、1クロックサイクル中に複数の命令を実行する事ができるプロセッサーです。
